Lattice-based cryptography is the generic term for constructions of cryptographic primitives that involve lattices, either in the construction itself or in the security proof. Lattice-based constructions are currently important candidates for post-quantum cryptography. Unlike more widely used and known public-key schemes such as the RSA, Diffie-Hellman or elliptic-curve cryptosystems, which are easily attacked by a quantum computer, some lattice-based constructions appear to be resistant to attack by both classical and quantum computers. Furthermore, many lattice-based constructions are considered to be secure under the assumption that certain well-studied computational lattice problems cannot be solved efficiently.

History[edit]

Rely on the notion of quantum one time pad (QOTP) that allows to information theoretically encrypt a quantum state using a single-use classical random pad. They propose to encrypt a quantum state using a QOTP, and then encrypt the pad itself using a classical homomorphic encryption scheme. SKM acts as a process awaiting key generation or key retrieval requests sent to it through a secure TCP/IP communication path between SKM and the tape library. When a new data encryption key is needed, the tape drive requests a key, which the library forwards to the primary SKM server.

IDQ’s Quantum Key Generation solutions ensure the creation of truly random encryption keys and unique digital tokens for highly secure crypto operations. They are based on the internationally tested and certified Quantis Quantum Random Number Generator. It has been replaced by the Advanced Encryption Standard – AES – which has a minimum key length of 128 bits4. In addition to its length, the amount of information encrypted with a given key also influences the strength of the scheme. In general, the more often a key is changed, the better the security. Quantum Resistant Public Key Cryptography Yongge Wang. We develop post-quantum (or quantum resistant) public key encryption techniques. Our first implementation is based on the Random Linear Code Based Public Key Encryption Shceme (RLCE) which was recently introduced by Dr. Generalized Quantum Shannon Impossibility for Quantum Encryption Ching-Yi Lai∗ and Kai-Min Chung Institute of Information Science, Academia Sinica, Taipei, 11529 Taiwan Abstract—The famous Shannon impossibility result says that any encryption scheme with perfect secrecy requires a secret key at least as longas the message. SKM acts as a process awaiting key generation or key retrieval requests sent to it through a secure TCP/IP communication path between SKM and the tape library. When a new data encryption key is needed, the tape drive requests a key, which the library forwards to the primary SKM server.

In 1996, Miklós Ajtai introduced the first lattice-based cryptographic construction whose security could be based on the hardness of well-studied lattice problems,^[1] and Cynthia Dwork showed that a certain average-case lattice problem, known as Short Integer Solutions (SIS), is at least as hard to solve as a worst-case lattice problem.^[2] He then showed a cryptographic hash function whose security is equivalent to the computational hardness of SIS

In 1998, Jeffrey Hoffstein, Jill Pipher, and Joseph H. Silverman introduced a lattice-based public-key encryption scheme, known as NTRU.^[3] However, their scheme is not known to be at least as hard as solving a worst-case lattice problem.

The first lattice-based public-key encryption scheme whose security was proven under worst-case hardness assumptions was introduced by Oded Regev in 2005,^[4] together with the Learning with Errors problem (LWE). Since then, much follow-up work has focused on improving Regev's security proof^[5][6] and improving the efficiency of the original scheme.^{[7][8][9][10]} Much more work has been devoted to constructing additional cryptographic primitives based on LWE and related problems. For example, in 2009, Craig Gentry introduced the first fully homomorphic encryption scheme, which was based on a lattice problem.^[11]

Mathematical background[edit]

A lattice${\displaystyle L\subset {\mathbb{R}}^n}$ is the set of all integer linear combinations of basis vectors ${\displaystyle {\mathbf{b}}_1,\dots ,{\mathbf{b}}_n\in {\mathbb{R}}^n}$. I.e., ${\displaystyle L=\{\sum a_i{\mathbf{b}}_i:a_i\in \mathbb{Z}\}.}$For example, ${\displaystyle {\mathbb{Z}}^n}$ is a lattice, generated by the standard orthonormal basis for ${\displaystyle {\mathbb{R}}^n}$. Crucially, the basis for a lattice is not unique. For example, the vectors ${\displaystyle (3,1,4)}$, ${\displaystyle (1,5,9)}$, and ${\displaystyle (2,-1,0)}$ form an alternative basis for ${\displaystyle {\mathbb{Z}}^3}$.

The most important lattice-based computational problem is the Shortest Vector Problem (SVP or sometimes GapSVP), which asks us to approximate the minimal Euclidean length of a non-zero lattice vector. This problem is thought to be hard to solve efficiently, even with approximation factors that are polynomial in ${\displaystyle n}$, and even with a quantum computer. Many (though not all) lattice-based cryptographic constructions are known to be secure if SVP is in fact hard in this regime.

Quantum Entanglement

Selected lattice-based cryptosystems[edit]

Encryption schemes[edit]

• Peikert's Ring - Learning With Errors (Ring-LWE) Key Exchange^[8]

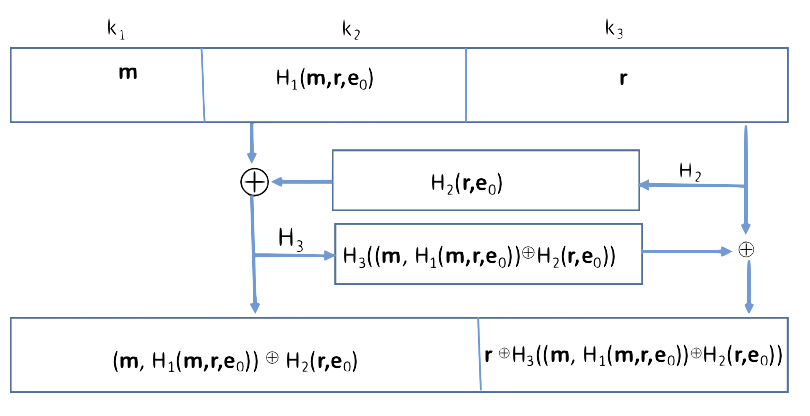
Signatures[edit]

• Güneysu, Lyubashevsky, and Poppleman's Ring - Learning with Errors (Ring-LWE) Signature^[12]

Hash functions[edit]

• LASH (Lattice Based Hash Function)^[13][14]

Fully homomorphic encryption[edit]

• Gentry's original scheme.^[11]
• Brakerski and Vaikuntanathan.^[15][16]

Security[edit]

Lattice-based cryptographic constructions are the leading candidates for public-keypost-quantum cryptography.^[17] Indeed, the main alternative forms of public-key cryptography are schemes based on the hardness of factoring and related problems and schemes based on the hardness of the discrete logarithm and related problems. However, both factoring and the discrete logarithm are known to be solvable in polynomial time on a quantum computer.^[18] Furthermore, algorithms for factorization tend to yield algorithms for discrete logarithm, and vice versa. This further motivates the study of constructions based on alternative assumptions, such as the hardness of lattice problems. Windows xp product key generator free download.

Many lattice-based cryptographic schemes are known to be secure assuming the worst-case hardness of certain lattice problems.^[1][4][5] I.e., if there exists an algorithm that can efficiently break the cryptographic scheme with non-negligible probability, then there exists an efficient algorithm that solves a certain lattice problem on any input. In contrast, cryptographic schemes based on, e.g., factoring would be broken if factoring was easy 'on an average input,' even if factoring was in fact hard in the worst case. However, for the more efficient and practical lattice-based constructions (such as schemes based on NTRU and even schemes based on LWE with more aggressive parameters), such worst-case hardness results are not known. For some schemes, worst-case hardness results are known only for certain structured lattices^[7] or not at all.

Functionality[edit]

For many cryptographic primitives, the only known constructions are based on lattices or closely related objects. These primitives include fully homomorphic encryption,^[11]indistinguishability obfuscation,^[19]cryptographic multilinear maps, and functional encryption.^[19]

See also[edit]

References[edit]

1. ^ ^abAjtai, Miklós (1996). 'Generating Hard Instances of Lattice Problems'. Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing. pp. 99–108. CiteSeerX10.1.1.40.2489. doi:10.1145/237814.237838. ISBN978-0-89791-785-8.
2. ^Public-Key Cryptosystem with Worst-Case/Average-Case Equivalence
3. ^Hoffstein, Jeffrey; Pipher, Jill; Silverman, Joseph H. (1998). 'NTRU: A ring-based public key cryptosystem'. Algorithmic Number Theory. Lecture Notes in Computer Science. 1423. pp. 267–288. CiteSeerX10.1.1.25.8422. doi:10.1007/bfb0054868. ISBN978-3-540-64657-0.
4. ^ ^abRegev, Oded (2005-01-01). 'On lattices, learning with errors, random linear codes, and cryptography'. Proceedings of the thirty-seventh annual ACM symposium on Theory of computing - STOC '05. ACM. pp. 84–93. CiteSeerX10.1.1.110.4776. doi:10.1145/1060590.1060603. ISBN978-1581139600.
5. ^ ^abPeikert, Chris (2009-01-01). 'Public-key cryptosystems from the worst-case shortest vector problem'. Proceedings of the 41st annual ACM symposium on Symposium on theory of computing - STOC '09. ACM. pp. 333–342. CiteSeerX10.1.1.168.270. doi:10.1145/1536414.1536461. ISBN9781605585062.
6. ^Brakerski, Zvika; Langlois, Adeline; Peikert, Chris; Regev, Oded; Stehlé, Damien (2013-01-01). 'Classical hardness of learning with errors'. Proceedings of the 45th annual ACM symposium on Symposium on theory of computing - STOC '13. ACM. pp. 575–584. arXiv:1306.0281. doi:10.1145/2488608.2488680. ISBN9781450320290.
7. ^ ^abLyubashevsky, Vadim; Peikert, Chris; Regev, Oded (2010-05-30). On Ideal Lattices and Learning with Errors over Rings. Advances in Cryptology – EUROCRYPT 2010. Lecture Notes in Computer Science. 6110. pp. 1–23. CiteSeerX10.1.1.352.8218. doi:10.1007/978-3-642-13190-5_1. ISBN978-3-642-13189-9.
8. ^ ^abPeikert, Chris (2014-07-16). 'Lattice Cryptography for the Internet'(PDF). IACR. Retrieved 2017-01-11.
9. ^Alkim, Erdem; Ducas, Léo; Pöppelmann, Thomas; Schwabe, Peter (2015-01-01). 'Post-quantum key exchange - a new hope'.Cite journal requires journal= (help)
10. ^Bos, Joppe; Costello, Craig; Ducas, Léo; Mironov, Ilya; Naehrig, Michael; Nikolaenko, Valeria; Raghunathan, Ananth; Stebila, Douglas (2016-01-01). 'Frodo: Take off the ring! Practical, Quantum-Secure Key Exchange from LWE'.Cite journal requires journal= (help)
11. ^ ^abcGentry, Craig (2009-01-01). A Fully Homomorphic Encryption Scheme (Thesis). Stanford, CA, USA: Stanford University.
12. ^Güneysu, Tim; Lyubashevsky, Vadim; Pöppelmann, Thomas (2012). 'Practical Lattice-Based Cryptography: A Signature Scheme for Embedded Systems'(PDF). Cryptographic Hardware and Embedded Systems – CHES 2012. Lecture Notes in Computer Science. 7428. IACR. pp. 530–547. doi:10.1007/978-3-642-33027-8_31. ISBN978-3-642-33026-1. Retrieved 2017-01-11.
13. ^'LASH: A Lattice Based Hash Function'. Archived from the original on October 16, 2008. Retrieved 2008-07-31.CS1 maint: BOT: original-url status unknown (link) (broken)
14. ^Scott Contini, Krystian Matusiewicz, Josef Pieprzyk, Ron Steinfeld, Jian Guo, San Ling and Huaxiong Wang (2008). 'Cryptanalysis of LASH'(PDF). Fast Software Encryption. Lecture Notes in Computer Science. 5086. pp. 207–223. doi:10.1007/978-3-540-71039-4_13. ISBN978-3-540-71038-7.CS1 maint: uses authors parameter (link)
15. ^Brakerski, Zvika; Vaikuntanathan, Vinod (2011). 'Efficient Fully Homomorphic Encryption from (Standard) LWE'.Cite journal requires journal= (help)
16. ^Brakerski, Zvika; Vaikuntanathan, Vinod (2013). 'Lattice-Based FHE as Secure as PKE'.Cite journal requires journal= (help)
17. ^Micciancio, Daniele; Regev, Oded (2008-07-22). 'Lattice-based cryptography'(PDF). Retrieved 2017-01-11.Cite journal requires journal= (help)
18. ^Shor, Peter W. (1997-10-01). 'Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer'. SIAM Journal on Computing. 26 (5): 1484–1509. arXiv:quant-ph/9508027. doi:10.1137/S0097539795293172. ISSN0097-5397.
19. ^ ^abGarg, Sanjam; Gentry, Craig; Halevi, Shai; Raykova, Mariana; Sahai, Amit; Waters, Brent (2013-01-01). 'Candidate Indistinguishability Obfuscation and Functional Encryption for all circuits'. CiteSeerX10.1.1.400.6501.Cite journal requires journal= (help)

Bibliography[edit]

• Oded Goldreich, Shafi Goldwasser, and Shai Halevi. 'Public-key cryptosystems from lattice reduction problems'. In CRYPTO ’97: Proceedings of the 17th Annual International Cryptology Conference on Advances in Cryptology, pages 112–131, London, UK, 1997. Springer-Verlag.
• Phong Q. Nguyen. 'Cryptanalysis of the Goldreich–Goldwasser–Halevi cryptosystem from crypto ’97'. In CRYPTO ’99: Proceedings of the 19th Annual International Cryptology Conference on Advances in Cryptology, pages 288–304, London, UK, 1999. Springer-Verlag.
• Oded Regev. Lattice-based cryptography. In Advances in cryptology (CRYPTO), pages 131–141, 2006.

Today’s connected world requires constantly higher levels of security. In many situations, this is done by relying on cryptography, for which one of the critical elements is the unpredictability of the encryption keys. Other security applications, like identity & access management, also require a strong cryptographic foundation based on unique tokens.

Keys are used for encryption of information as well as in other cryptographic schemes; such as digital signatures, personal identification and message authentication codes. They are used everywhere in modern digital communications and they enable the trust which underpins communications in our globalised world, including the internet and financial systems.

The security of these keys or digital tokens lies in the quality of the randomness used to create the key itself. If the random number generation and the processes surrounding it are weak, then the key can easily be copied, forged or guessed and the security of the entire system is compromised. Therefore, high-quality key generation that ensures unpredictable, random keys is critical for security.

Digital or paper currencies also require unique identifiers that cannot be easily guessed or forecast. Also, many other high-value applications like lotteries, or gaming in general, require the same capacity to generate totally unpredictable numbers. The common denominator of all these markets is the critical reliance on absolutely random numbers.

Private Key Encryption Scheme

For more information, read our blog: The Case for Strong Encryption Keys.

Secrecy of the encryption keys

Today, best security practices are based on the assumption that an attacker has in-depth knowledge of the cryptographic algorithm, and that the security of the system resides primarily in the secrecy of the encryption key. This is known as Kerckhoff’s principle “only secrecy of the key provides security”, or, reformulated as Shannon’s maxim ”The enemy knows the system”.

According to security expert Bruce Schneier: “The reasoning behind Kerckhoffs’ principle is compelling. If the cryptographic algorithm must remain secret in order for the system to be secure, then the system is less secure. The system is less secure, because security is affected if the algorithm falls into enemy hands. It’s harder to set up different communications nets, because it would be necessary to change algorithms as well as keys. The resultant system is more fragile, simply because there are more secrets that need to be kept. In a well-designed system, only the key needs to be secret; in fact, everything else should be assumed to be public.”

The history of cryptography provides compelling evidence that keeping a cryptographic system secret is nearly impossible over any long period of time, evidenced by the well documented cracking of the Enigma machine and other cases. While many governments do use elements of “security through obscurity” to enhance defence in depth, they also focus very heavily on ensuring that the encryption key is protected. And Schneier continues: “If the algorithm or protocol or implementation needs to be kept secret, then it is really part of the key and should be treated as such.”

The key is the cornerstone of secure cryptosystems and are used to ensure:

Requirements of the encryption key

So it is clear that the security of any crypto-based system depends fundamentally on the security and quality of the underlying encryption key. And yet is surprising in today’s world just how weak many of these keys are, and how little attention is paid to the key generation process. To provide adequate security the key must be:

While these attributes – uniqueness and randomness – are easy to assume, they are actually complex to ensure and even more complex to test. There have been many cases recently where the keys underlying crypto-systems have been proven to be weak, either by accident or by design. According to Schneier, one such attack could “reduce the amount of entropy from 128 bits to 32 bits. This could be done without failing any randomness tests.”

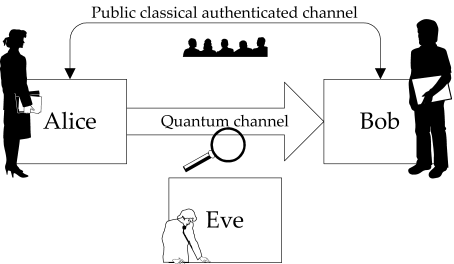
Classical versus Quantum Random Number Generators

Two families of physical processes can be used for randomness generation:

Processes based on classical physics

As classical physics is fundamentally deterministic, it should in principle be impossible to generate random numbers using it. In practice though, there exist processes that exhibit complex evolutions, which make them difficult or even impossible to predict. This unpredictability arises from the influence of the environment on the process and/or the indefiniteness of the initial conditions (chaotic processes).

RNG based on classical physics processes exploit these sources of unpredictability. The randomness of the generated bits cannot be proven but only inferred after empirical testing of assumptions. Established standards for the qualification of physical RNGs (notably the German BSI AIS 31 standard) call for on the fly testing of the output of these devices to detect a possible failure. Running live statistical tests is difficult as they require a large amount of bits to yield significant results (108 or 109 bits), which is costly in case of a hardware implementation.

Finally, in security applications it is always important to take into account a possible functional problem with the system and to ensure a so called “graceful failure”. With classical physics based RNGs, this is very difficult as the failure modes of the underlying process are difficult to model.

Processes based on quantum physics

Contrary to classical physics, quantum physics is fundamentally random. There exist processes whose unpredictability is fundamental and can be proven.

The possibility to model the quantum process and prove its randomness is essential in two respects. First, it allows to identify critical parameters, which can then be monitored live to guarantee ex-ante the quality of the random bits produced. This property allows to reduce or even suppress the need for live statistical testing of the output stream.

The second important advantage related to the use of a quantum process is that its failure modes can be modelled and evaluated. This allows to design RNGs which “fail gracefully”, ensuring for example the inhibition of the random bit stream in case of failure, instead of producing imperfect random numbers. Given the fact that quantum physics describes the behaviour of the fundamental building blocks (atoms, particles, etc.) of the physical world, one could argue that everything is quantum and consequently classical physics based RNGs are also quantum.

One could for example say that for a RNG based on thermal noise in an electronic component, this noise is also quantum. This view has some merit, but this noise could be considered as dirty quantum, as it consists of a large ensemble of quantum processes, which interact together. Because of this, the process does not capture the fundamental randomness of an elementary quantum process. There exists good RNGs based on classical physics, but all one can say about them is that they produce a stream which is probably random. On the contrary, the bit stream produced by a quantum RNG (QRNG) is provably random.

Our solutions

IDQ’s Quantum Key Generation solutions ensure the creation of truly random encryption keys and unique digital tokens for highly secure crypto operations. They are based on the internationally tested and certified Quantis Quantum Random Number Generator. Used by governments and enterprises worldwide, they offer the guarantee of Swiss quality, neutrality and trust.

The Quantis Appliance is a device providing randomness in networked, high availability environments. The Quantum Key Factory is a platform which allows for a combination of multiple sources of randomness (entropy), as well as best practice key scheduling, key mixing, key storage and key auditing to guarantee secure key generation at the highest level of trust.

Benefits

For more information, read our blog: The Case for Strong Encryption Keys.