Diffie-hellman Dh Key How Long Generate
If you like this post, you might like my book: API Security in Action (use discount code fccmadden to get 37% off when ordering).
To get a larger Ephemeral DH key length than 768 bits you need to be running on Java 8. 1024 is the new default, and you can go up to 2048 using the jdk.tls.ephemeralDHKeySize (details: customising DH keys). From what I could find, there is no concept of regenerating the key parameters separately in Java. When going from 2048-bit to 4096-bit, the density of strong primes is divided by 4, and the primality tests will also be about 4 times slower, so if generating a 2048-bit DH modulus takes 1 hour on average, the same machine with the same software will use an average of 16 hours for a 4096-bit DH modulus. But Diffie-Hellman is a key exchange algorithm, not an encryption algorithm. DH isn't for doing asymmetric encryption or signature, it generates a shared secret. The shared secret can be used for encryption, but then it's symmetric encryption (e.g. $endgroup$ – Gilles 'SO- stop being evil' Sep 24 '15 at 15:08.
Update 2 (17th May, 2017): I’ve written some notes on correctly validating ECDH public keys.
Update (20th April, 2017): I’ve noticed that this article gets by far the most daily hits on my blog. This worries me that people are using this code as a template for building real ECDHE key agreement, when it was only intended as a guide to the Java API. There are a lot of details in safe construction of such a protocol. More secure alternatives than to trying to roll this yourself include the various complete protocols listed at the end of the article. With that said, we’ll get back to the original article:
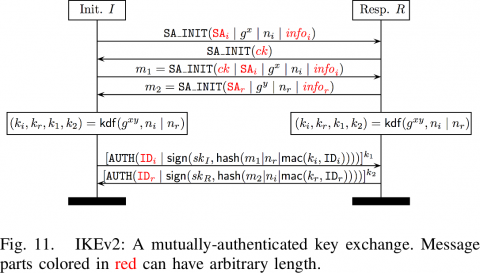
Diffie-Hellman—A public-key cryptography protocol that allows two parties to establish a shared secret over an unsecure communications channel. Diffie-Hellman is used within IKE to establish session keys. It supports 768-bit (the default), 1024-bit, 1536-bit, 2048-bit, 3072-bit, and 4096-bit DH groups.
Diffie-Hellman key agreement (DH) is a way for two parties to agree on a symmetric secret key without explicitly communicating that secret key. As such, it provides a way for the parties to negotiate a shared AES cipher key or HMAC shared secret over a potentially insecure channel. It does not by itself provide authentication, however, so it is vulnerable to man-in-the-middle attacks without additional measures. There are several ways to provide these additional measures (e.g. signing the ephemeral public keys using a CA-issued certificate, or using a protocol like OTR), but we will not discuss them here, or go into the details of how the key agreement works. Java provides support out-of-the-box for both original discrete log DH and elliptic curve (ECDH) key agreement protocols, although the latter may not be supported on all JREs. ECDH should be preferred for any new applications as it provides significantly improved security for reasonable key sizes.
As is often the case in Java, the use of these classes can be a bit convoluted. Here we demonstrate simple Java code for ECDH key agreement on the command line. We only demonstrate ephemeral key agreement, in which the two parties generate unique public/private key pairs at the start of the protocol and throw them away once the shared secret has been negotiated. This can form the basis for perfect forward secrecy.
WARNING: the code here is not a complete security protocol and should be used for reference on the Java API only.
The Code
The complete code example is as follows:
To use the example, compile it and then run two instances of it (possibly on different computers). It will print out a hex-encoded ephemeral public key value and then wait for the public key from the other instance. Simply copy+paste this values from one to the other (and vice-versa) and then it will print out the computed shared secret, again hex-encoded and finally a secret key derived from the shared secret.
Let’s walk through the example step-by-step. Firstly, we import a vast number of different classes. We’ll discuss what all of these are for when we get to them.
Step 1: Generate ephemeral ECDH key pair
The first step is to generate an ephemeral elliptic curve key pair for use in the algorithm. We do this using the aptly-named KeyPairGenerator using the “EC” algorithm name to select Elliptic Curve key generation:
By setting the key size to 256-bits, Java will select the NIST P-256 curve parameters (secp256r1). For other key sizes, it will choose other NIST standard curves, e.g. P-384, P-521. If you wish to use different parameters, then you must specify them explicitly using the ECGenParameterSpec argument.
Step 2: Exchange the public keys
The next step is to send our public key to the other party and to receive their public key. In this case, we achieve this by simply printing them out and requiring a human being to perform the communication. No authentication is performed. This means that we cannot be sure that the public key we received is really from the other party and not from a man-in-the-middle.
We assume that the other party is also using a NIST P-256 curve public key. We also assume that the output of PublicKey.getEncoded() is an X.509-encoded key. This turns out to be true in the Oracle JRE, but I cannot find any documented guarantee of this behaviour. A more robust approach would be to communicate the ECPoint and ECParameterSpec of the public key, and use an ECPublicKeySpec to reconstruct the key, but that is even more work.
Step 3: Perform key agreement
The actual ECDH key agreement is straightforward once we have exchanged public keys.
We grab an instance of the ECDH key agreement protocol. The first step is to initialise it with our private key. Then we pass it the other party’s public key via the doPhase() method. We pass true as the second argument to indicate that this is the last phase of the agreement (it is the only phase in ECDH). Diffie-Hellman works by calculating a shared secret based on our private key and the other party’s public key, so this is all we need in this case. The magic of DH is that each party will calculate the same value despite having different sets of keys available to them. Nobody listening in on the exchange can calculate the shared secret unless they have access to one of the private keys (which are never communicated).
Step 4: Extract the shared secret and derive keys
Diffie-hellman Dh Key How Long Generate Data
The final step is to extract the shared secret and then derive a key from it.
Note that it is not advisable to use the shared secret directly as a symmetric key for various reasons. In particular, while the derived secret is indistinguishable from a randomly selected element from the set of all possible outputs of the elliptic curve group, this is not the same thing as a uniformly random string of bits. Viewed as a string of bits, it will have some structure to it. Put another way, the P-256 curve provides roughly equivalent security to a 128-bit secret key, yet the output shared secret is 256 bits. This reveals that the shared secret does not really provide 256 bits of “random” key data. There are further reasons for not using the shared secret directly, depending on the usage. For instance, the security considerations section of RFC 7748 advises to derive a key from the shared secret plus both public keys if we intend to use the key for authentication (this RFC uses different curves than we use here, but it is good advice regardless):
Designers using these curves should be aware that for each public
key, there are several publicly computable public keys that are
equivalent to it, i.e., they produce the same shared secrets. Thus
using a public key as an identifier and knowledge of a shared secret
as proof of ownership (without including the public keys in the key
derivation) might lead to subtle vulnerabilities.
We adopt the approach described in the libsodium documentation, of deriving a key by hashing the shared secret and both public keys, but using SHA-256 rather than BLAKE2. These choices of algorithms and curves are purely for convenience because they are readily available on the JVM without 3rd party libraries (e.g. Bouncy Castle). The only trickiness is to ensure that we feed the public keys into the hash in the same order on both sides of the agreement protocol. For simplicity, we do this by just sorting them lexicographically.
Et voila! Both parties now have the same derived key, which can be used for an AES cipher or HMAC key or however you wish. A more sophisticated key derivation function, such as HKDF, can be used to derive further keys (for instance, separate keys sending data in each direction, which is recommended).
There are a number of complete protocols that build upon this basic agreement mechanism, adding authentication and other details:
- TLS includes this as the various ECDHE_ cipher suites, such as ECDHE_ECDSA_WITH_AES256_GCM_SHA384 (in TLS 1.2 or earlier, TLS 1.3 cipher suites only specify the symmetric encryption component, with key agreement and authentication being negotiated via extensions instead), which means ephemeral ECDH where the exchanged ephemeral public keys are signed using long-term ECDSA keys to provide authentication, and then using the derived secret as a 256-bit key for AES-GCM authenticated encryption. TLS 1.3 mandates cipher suites that support forward-secrecy, including ECDHE. It also has some optimisations to reduce the overhead of the TLS ECDHE handshake, including support for “0-RTT” (zero round-trip time) that allows a client that has previously talked to a server to start a new session and send encrypted traffic on the very first message.
- Protocols like Noise or CurveCP (or CurveZMQ).
- The JSON Web Token (JWT) specs describe a ECDH-ES (ephemeral-static) key agreement and key derivation approach. In this case the recipient has a long-term (static) public key and the sender uses an ephemeral key-pair. This allows the recipient to immediately send a message, without an interactive handshake (i.e., the recipient can be offline, as in email), and it also authenticates the recipient if the long-term public key can be trusted (e.g. via a CA signature, web of trust, etc). However, it gives up forward secrecy, as any compromise of the recipient’s long-term private key will allow decryption of all previous messages sent to that recipient under that key pair. It should be possible to build something like TLS’s 0-RTT mechanism on top of this, but I don’t know of a fully worked out design (and I wouldn’t attempt it unless you know what you are doing).
Diffie-hellman Dh Key How Long Generate Data
Definition
Provides a Cryptography Next Generation (CNG) implementation of the Elliptic Curve Diffie-Hellman (ECDH) algorithm. This class is used to perform cryptographic operations.
Diffie-hellman Dh Key How Long Generate Money
Examples
Diffie-hellman Dh Key How Long Generate Pdf
The following example shows how to use the ECDiffieHellmanCng class to establish a key exchange and how to use that key to encrypt a message that can be sent over a public channel and decrypted by the receiver.
Remarks
The ECDiffieHellmanCng class enables two parties to exchange private key material even if they are communicating through a public channel. Both parties can calculate the same secret value, which is referred to as the secret agreement in the managed Diffie-Hellman classes. The secret agreement can then be used for a variety of purposes, including as a symmetric key. However, instead of exposing the secret agreement directly, the ECDiffieHellmanCng class does some post-processing on the agreement before providing the value. This post processing is referred to as the key derivation function (KDF); you can select which KDF you want to use and set its parameters through a set of properties on the instance of the Diffie-Hellman object.
| Key derivation function | Properties |
|---|---|
| Hash | HashAlgorithm - The hash algorithm that is used to process the secret agreement. SecretPrepend - An optional byte array to prepend to the secret agreement before hashing it. SecretAppend - An optional byte array to append to the secret agreement before hashing it. |
| Hmac | HashAlgorithm - The hash algorithm that is used to process the secret agreement. SecretPrepend- An optional byte array to prepend to the secret agreement before hashing it. SecretAppend - An optional byte array to append to the secret agreement before hashing it. |
| Tls | Label - The label for key derivation. Seed - The seed for key derivation. |
The result of passing the secret agreement through the key derivation function is a byte array that may be used as key material for your application. The number of bytes of key material generated is dependent on the key derivation function; for example, SHA-256 will generate 256 bits of key material, whereas SHA-512 will generate 512 bits of key material.The basic flow of an ECDH key exchange is as follows:
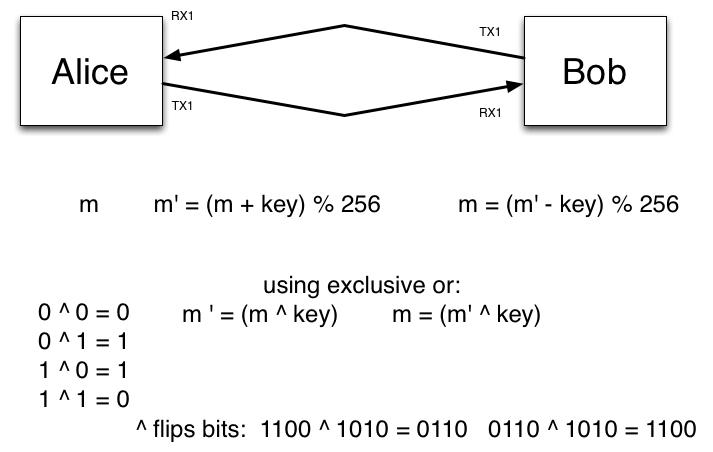
Alice and Bob create a key pair to use for the Diffie-Hellman key exchange operation
Alice and Bob configure the KDF using parameters the agree on.
Alice sends Bob her public key.
Bob sends Alice his public key.
Alice and Bob use each other's public keys to generate the secret agreement, and apply the KDF to the secret agreement to generate key material.
Constructors
| ECDiffieHellmanCng() | Initializes a new instance of the ECDiffieHellmanCng class with a random key pair. |
| ECDiffieHellmanCng(CngKey) | Initializes a new instance of the ECDiffieHellmanCng class by using the specified CngKey object. |
| ECDiffieHellmanCng(ECCurve) | Creates a new instance of the ECDiffieHellmanCng class whose public/private key pair is generated over the specified curve. |
| ECDiffieHellmanCng(Int32) | Initializes a new instance of the ECDiffieHellmanCng class with a random key pair, using the specified key size. |
Fields
| KeySizeValue | Represents the size, in bits, of the key modulus used by the asymmetric algorithm. (Inherited from AsymmetricAlgorithm) |
| LegalKeySizesValue | Specifies the key sizes that are supported by the asymmetric algorithm. (Inherited from AsymmetricAlgorithm) |
Properties
| HashAlgorithm | Gets or sets the hash algorithm to use when generating key material. |
| HmacKey | Gets or sets the Hash-based Message Authentication Code (HMAC) key to use when deriving key material. |
| Key | Specifies the CngKey that is used by the current object for cryptographic operations. |
| KeyDerivationFunction | Gets or sets the key derivation function for the ECDiffieHellmanCng class. |
| KeyExchangeAlgorithm | Gets the name of the key exchange algorithm. (Inherited from ECDiffieHellman) |
| KeySize | Gets or sets the size, in bits, of the key modulus used by the asymmetric algorithm. |
| Label | Gets or sets the label value that is used for key derivation. |
| LegalKeySizes | Gets the key sizes that are supported by the asymmetric algorithm. (Inherited from AsymmetricAlgorithm) |
| PublicKey | Gets the public key that can be used by another ECDiffieHellmanCng object to generate a shared secret agreement. |
| SecretAppend | Gets or sets a value that will be appended to the secret agreement when generating key material. |
| SecretPrepend | Gets or sets a value that will be added to the beginning of the secret agreement when deriving key material. |
| Seed | Gets or sets the seed value that will be used when deriving key material. |
| SignatureAlgorithm | Gets the name of the signature algorithm. (Inherited from ECDiffieHellman) |
| UseSecretAgreementAsHmacKey | Gets a value that indicates whether the secret agreement is used as a Hash-based Message Authentication Code (HMAC) key to derive key material. |
Methods
| Clear() | Releases all resources used by the AsymmetricAlgorithm class. (Inherited from AsymmetricAlgorithm) |
| DeriveKeyFromHash(ECDiffieHellmanPublicKey, HashAlgorithmName) | Performs key derivation using a specified hash algorithm. (Inherited from ECDiffieHellman) |
| DeriveKeyFromHash(ECDiffieHellmanPublicKey, HashAlgorithmName, Byte[], Byte[]) | Performs key derivation using a specified hash algorithm with optional prepended or appended data. |
| DeriveKeyFromHmac(ECDiffieHellmanPublicKey, HashAlgorithmName, Byte[]) | Performs key derivation using a specified HMAC (Hash-based Message Authentication Code) algorithm. (Inherited from ECDiffieHellman) |
| DeriveKeyFromHmac(ECDiffieHellmanPublicKey, HashAlgorithmName, Byte[], Byte[], Byte[]) | Performs key derivation using a specified HMAC (Hash-based Message Authentication Code) algorithm with optional prepended or appended data. |
| DeriveKeyMaterial(CngKey) | Derives the key material that is generated from the secret agreement between two parties, given a CngKey object that contains the second party's public key. |
| DeriveKeyMaterial(ECDiffieHellmanPublicKey) | Derives the key material that is generated from the secret agreement between two parties, given an ECDiffieHellmanPublicKey object that contains the second party's public key. |
| DeriveKeyTls(ECDiffieHellmanPublicKey, Byte[], Byte[]) | Performs key derivation using the TLS (Transport Layer Security) 1.1 PRF (Pseudo-Random Function). |
| DeriveSecretAgreementHandle(CngKey) | Gets a handle to the secret agreement generated between two parties, given a CngKey object that contains the second party's public key. |
| DeriveSecretAgreementHandle(ECDiffieHellmanPublicKey) | Gets a handle to the secret agreement generated between two parties, given an ECDiffieHellmanPublicKey object that contains the second party's public key. |
| Dispose() | Releases all resources used by the current instance of the AsymmetricAlgorithm class. (Inherited from AsymmetricAlgorithm) |
| Dispose(Boolean) | Releases the unmanaged resources used by the AsymmetricAlgorithm class and optionally releases the managed resources. (Inherited from AsymmetricAlgorithm) |
| Equals(Object) | Determines whether the specified object is equal to the current object. (Inherited from Object) |
| ExportECPrivateKey() | Exports the current key in the ECPrivateKey format. (Inherited from ECDiffieHellman) |
| ExportEncryptedPkcs8PrivateKey(ReadOnlySpan<Byte>, PbeParameters) | Exports the current key in the PKCS#8 EncryptedPrivateKeyInfo format with a byte-based password. (Inherited from AsymmetricAlgorithm) |
| ExportEncryptedPkcs8PrivateKey(ReadOnlySpan<Char>, PbeParameters) | Exports the current key in the PKCS#8 EncryptedPrivateKeyInfo format with a char-based password. (Inherited from AsymmetricAlgorithm) |
| ExportExplicitParameters(Boolean) | Exports the key and explicit curve parameters used by the ECCurve object into an ECParameters object. |
| ExportParameters(Boolean) | Exports the key used by the ECCurve object into an ECParameters object. |
| ExportPkcs8PrivateKey() | Exports the current key in the PKCS#8 PrivateKeyInfo format. (Inherited from AsymmetricAlgorithm) |
| ExportSubjectPublicKeyInfo() | Exports the public-key portion of the current key in the X.509 SubjectPublicKeyInfo format. (Inherited from AsymmetricAlgorithm) |
| FromXmlString(String) | This method is not implemented. |
| FromXmlString(String, ECKeyXmlFormat) | Deserializes the key information from an XML string by using the specified format. |
| GenerateKey(ECCurve) | Generates a new ephemeral public/private key pair for the specified curve. |
| GetHashCode() | Serves as the default hash function. (Inherited from Object) |
| GetType() | Gets the Type of the current instance. (Inherited from Object) |
| ImportECPrivateKey(ReadOnlySpan<Byte>, Int32) | Imports the public/private keypair from an ECPrivateKey structure, replacing the keys for this object. (Inherited from ECDiffieHellman) |
| ImportEncryptedPkcs8PrivateKey(ReadOnlySpan<Byte>, ReadOnlySpan<Byte>, Int32) | Imports the public/private keypair from a PKCS#8 EncryptedPrivateKeyInfo structure after decrypting with a byte-based password, replacing the keys for this object. (Inherited from ECDiffieHellman) |
| ImportEncryptedPkcs8PrivateKey(ReadOnlySpan<Char>, ReadOnlySpan<Byte>, Int32) | Imports the public/private keypair from a PKCS#8 EncryptedPrivateKeyInfo structure after decrypting with a char-based password, replacing the keys for this object. (Inherited from ECDiffieHellman) |
| ImportParameters(ECParameters) | Imports the specified parameters for an ECCurve object as a key into the current instance. |
| ImportPkcs8PrivateKey(ReadOnlySpan<Byte>, Int32) | Imports the public/private keypair from a PKCS#8 PrivateKeyInfo structure after decryption, replacing the keys for this object. (Inherited from ECDiffieHellman) |
| ImportSubjectPublicKeyInfo(ReadOnlySpan<Byte>, Int32) | Imports the public key from an X.509 SubjectPublicKeyInfo structure after decryption, replacing the keys for this object. (Inherited from ECDiffieHellman) |
| MemberwiseClone() | Creates a shallow copy of the current Object. (Inherited from Object) |
| ToString() | Returns a string that represents the current object. (Inherited from Object) |
| ToXmlString(Boolean) | This method is not implemented. |
| ToXmlString(ECKeyXmlFormat) | Serializes the key information to an XML string by using the specified format. |
| TryExportECPrivateKey(Span<Byte>, Int32) | Attempts to export the current key in the ECPrivateKey format into a provided buffer. (Inherited from ECDiffieHellman) |
| TryExportEncryptedPkcs8PrivateKey(ReadOnlySpan<Byte>, PbeParameters, Span<Byte>, Int32) | Attempts to export the current key in the PKCS#8 EncryptedPrivateKeyInfo format into a provided buffer, using a byte-based password. (Inherited from ECDiffieHellman) |
| TryExportEncryptedPkcs8PrivateKey(ReadOnlySpan<Char>, PbeParameters, Span<Byte>, Int32) | Attempts to export the current key in the PKCS#8 EncryptedPrivateKeyInfo format into a provided buffer, using a char-based password. (Inherited from ECDiffieHellman) |
| TryExportPkcs8PrivateKey(Span<Byte>, Int32) | Attempts to export the current key in the PKCS#8 PrivateKeyInfo format into a provided buffer. (Inherited from ECDiffieHellman) |
| TryExportSubjectPublicKeyInfo(Span<Byte>, Int32) | Attempts to export the current key in the X.509 SubjectPublicKeyInfo format into a provided buffer. (Inherited from ECDiffieHellman) |
Explicit Interface Implementations
Diffie Hellman Explained
| IDisposable.Dispose() | For a description of this member, see Dispose(). (Inherited from AsymmetricAlgorithm) |